

|
ПОИСК ГЛОБАЛЬНОГО ОПТИМУМА ДЛЯ ЗАДАЧ ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ СИСТЕМ ИЛИ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНЫХ ЗАКОНОВ УПРАВЛЕНИЯ.
|
ИСПОЛЬЗОВАНИЕ
Под объектом оптимизации можно рассматривать что угодно. Главным показателем для возможности исследования оптимума это взаимосвязь между воздействием и реакцией, которая описывается с учетом основных свойств и функциональных возможностей объекта.
Поиск оптимального решения может быть выполнен несколькими путями (рис. 1):
- Математическая модель-->Поиск оптимума (ММ-->ПО)
- Экспериментальные исследования и регрессионный анализ-->Математическая модель-->Поиск оптимума (ЭИРА-->ММ-->ПО)
- Численное моделирование-->Экспериментальные исследования и регрессионный анализ-->Математическая модель-->Поиск оптимума (ЧМ-->ЭИРА-->ММ-->ПО)
- Численное моделирование-->Поиск оптимума (ЧМ-->ПО)
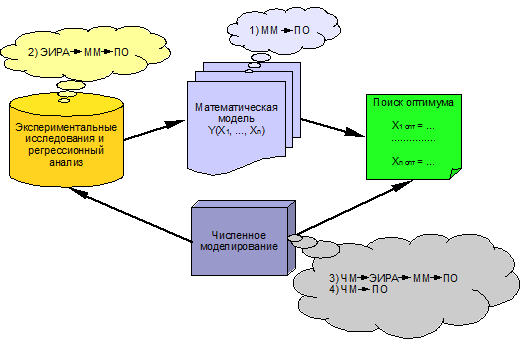
Рис. 1.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Для описания объекта оптимизации используеться структура данных которая описывает математически исследуемый объект и задает начальные, граничные условия, а также критерий поиска глобального оптимума. Модель описывается по правилам создания классов для языка програмирования Java (наследует класс OptimizationModelObject) и имеет следующую структуру:
public class test_001 extends OptimizationModelObject{
// Интервалы входных параметров
private float[][] interval_x = {
{48.0f, 112.0f},
{20.7f, 62.1f},
{3.0f, 5.0f},
};
// Метод возвращает масив с интервала входных параметров
public float[][] get_interval(){ return interval_x; }
// Метод возвращает значение дискретизации области входных параметров
public int get_digitization_area_values(){ return 3; }
// Метод возвращает значение дискретизации области значений
public int get_digitization_values(){ return 100; }
// Метод возвращает значение относительной точности
public float get_precision(){ return 0.001f; }
// Метод возвращает значение критерия оптимизации
// Минимум = -Double.MAX_VALUE
// Максимум = Double.MAX_VALUE
public double get_criterion_optimization(){ return -Double.MAX_VALUE; }
// Метод используется для включения(true) / выключения(false) вывода на экран промежуточных расчетов
public boolean is_debug(){return false;}
// Метод описывает модель и возвращает значение параметра оптимизации
// X - масив входных параметров
public double function(double[] X){
double y = 0.3000000019868215 -0.17749999463558197*(X[0]-48.0)/64.0 + 0.1262500025331974*(X[1]-20.7)/41.399998 + 0.14874999597668648*(X[2]-3.0)/2.0 -0.14750000089406967*(X[0]-48.0)/64.0*(X[0]-20.7)/41.399998 -0.16249998658895493*(X[0]-48.0)/64.0*(X[0]-3.0)/2.0 + 0.06499999761581421*(X[1]-20.7)/41.399998*(X[1]-3.0)/2.0 + 0.11000000437100729*Math.pow((X[0]-48.0)/64.0,2) + 0.022500005861123412*Math.pow((X[1]-20.7)/41.399998,2) + 0.0774999832113584*Math.pow((X[2]-3.0)/2.0,2);
return y;
}
}
После описания модели в ее сохраняют в файле с именем класса test_001.* и расширением *.java (test_001.java). Полученный файл модели (test_001.java) необходимо откомпелировать используя команду:
для Windows - javac -cp .;OptimizationModel.jar test_001.java
для Linux/Unix - javac -cp .:OptimizationModel.jar test_001.java
При успешной компиляции будет создан файл с тем же именем test_001.* и с расширением *.class (test_001.class).
ПОИСК ГЛОБАЛЬНОГО ОПТИМУМА
Для запуска поиска глобального оптимума достаточно использовать команду с консоли java [CLASSPATH] OptimizationModelSolver [SOLVER] <MODEL>
где:
CLASSPATH - параметр описывает путь к библиотеке OptimizationModel.jar;
SOLVER - параметр указывает какую методику использовать (aam aaqm gzm), если ни один парамтр не указан тогда используются все методики;
MODEL - имя файла математической модели.
Пример поиска глобального оптимума для модели - test_001
Операционная система
|
Командная строка
|
| Windows |
java -cp .;OptimizationModel.jar OptimizationModelSolver test_001 |
| Linux/Unix |
java -cp .:OptimizationModel.jar OptimizationModelSolver test_001 |
При запуске OptimizationModelSolver будет проведен поиск глобального оптимума с использованием нескольких методик.
Результат расчета примера модели test_001 представлен ниже.
*** Start optimization ***
Sat Mar 20 04:51:59 EET 2010
Number of processors/thread: 2/4
Loading model: test_pe_001_1269053514510
Thread: 33-48 (time: 3) Y(X1, ..., Xn) = -8.94903307855923
Thread: 49-64 (time: 4) Y(X1, ..., Xn) = -4.684240944984636
Thread: 17-32 (time: 4) Y(X1, ..., Xn) = -8.94903307855923
Thread: 1-16 (time: 4) Y(X1, ..., Xn) = -8.94903307855923
Solver: AAQM
Solving time (hh:mm:ss) 00:00:00 (total: 4 ms)
Matrix of parameters of model
X1 = 48.0 ... 112.0
X2 = 20.7 ... 62.1
X3 = 3.0 ... 5.0
Optimal Result for Y(X1, ..., Xn) = -8.94903307855923
X1 = 112.0 X2 = 20.700000762939453 X3 = 3.0
*** End optimization ***
*** Start optimization ***
Sat Mar 20 04:51:59 EET 2010
Number of processors/thread: 2/4
Loading model: test_pe_001_1269053514510
Thread: 17-32 (time: 2) Y(X1, ..., Xn) = -8.94903307855923
Thread: 1-16 (time: 2) Y(X1, ..., Xn) = -8.94903307855923
Thread: 33-48 (time: 2) Y(X1, ..., Xn) = -8.94903307855923
Thread: 49-64 (time: 5) Y(X1, ..., Xn) = -4.684240944984636
Solver: AAM
Solving time (hh:mm:ss) 00:00:00 (total: 5 ms)
Matrix of parameters of model
X1 = 48.0 ... 112.0
X2 = 20.7 ... 62.1
X3 = 3.0 ... 5.0
Optimal Result for Y(X1, ..., Xn) = -8.94903307855923
X1 = 112.0 X2 = 20.700000762939453 X3 = 3.0
*** End optimization ***
*** Start optimization ***
Sat Mar 20 04:51:59 EET 2010
Number of processors/thread: 2/4
Loading model: test_pe_001_1269053514510
Thread: 33-48 (time: 31) Y(X1, ..., Xn) = -8.94903307855892
Thread: 17-32 (time: 54) Y(X1, ..., Xn) = -8.94903307855892
Thread: 49-64 (time: 30) Y(X1, ..., Xn) = -8.94903307855892
Thread: 1-16 (time: 28) Y(X1, ..., Xn) = -8.94903307855892
Solver: GZM
Solving time (hh:mm:ss) 00:00:00 (total: 54 ms)
Matrix of parameters of model
X1 = 48.0 ... 112.0
X2 = 20.7 ... 62.1
X3 = 3.0 ... 5.0
Optimal Result for Y(X1, ..., Xn) = -8.94903307855892
X1 = 111.99999999999864 X2 = 20.700000762939453 X3 = 3.0
*** End optimization ***
В результате расчета примера модели test_001 для функции Y(X1, X2, X3)=... найдены значения Х1, Х2, Х3 при которых Y стримится к минимуму.
| Методика |
X1 |
X2 |
X3 |
Время решения |
Количество итераций |
| aaqm |
112.0 |
20.700000762939453 |
3.0 |
4 ms |
384 |
| aam |
112.0 |
20.700000762939453 |
3.0 |
5 ms |
768 |
| gzm |
111.99999999999864 |
20.700000762939453 |
3.0 |
54 ms |
134912 |


